Hvad er ICM og hvordan skal man udnytte det til sin fordel?

Dansk Poker har været så heldig at få Marcus Wuttke til at hjælpe os med at forstå hvad ICM er, hvorfor man som big stack kan udnytte det i specielle endgame situationer og hvad man bør tænke på, når man tager ICM i betragtning i turneringer. God fornøjelse!

I dag skal vi have et lille crash course i ICM

Vi starter med en overordnet introduktion til, hvad ICM er, hvordan man kan tilpasse sit spil derefter, og afslutningsvis laver vi nogle beregninger ud fra et finalebords-scenarie. Forhåbentlig er der noget for spillere på alle niveauer at tage med sig til deres eget spil.

Introduktion til ICM

Når du er i en hånd mod en modstander, der dækker dig (altså har flere chips), og du dermed risikerer at blive slået ud, bliver du nødt til at spille mere passivt. Dette skyldes, at så længe du overlever, har du mulighed for at klatre op i præmierne, når andre spillere ryger ud. Derfor er en fordobling af din chipstack ikke det samme som at fordoble din forventede pengemæssige værdi. Chips har en faldende penge-værdi – hver chip er mere værd, når du er shortstack, og mindre værd, når du er bigstack.

Af samme grund kan en bigstack, der dækker sine modstandere, spille mere aggressivt, da man kan lægge ekstra pres på dem via ICM. ICM-presset er størst i hænder mellem en mellemstack og en bigstack, fordi mellemstacken har mest at tabe – ved bare at folde kan de potentielt klatre i præmierne.

ICM er relevant hele vejen gennem en turnering indtil heads-up, men det er vigtigst ved boblen og på eller tæt på finalebordet.

Tilpasning af strategi til ICM

ICM handler ikke kun om all-in og calling ranges preflop. Det gælder også f.eks. hvor bredt du forsvarer din big blind. Hvis du har sværere ved at spille hånden postflop, kan det i mange tilfælde være bedre at folde direkte.

Et eksempel:
Lad os sige, der er rimeligt højt (men ikke ekstremt) ICM-pres. Du sidder med 22bb i big blind mod et min-raise fra UTG, som er chipleader. I det scenarie vil jeg hellere forsvare med 44 end med QJo. Grunden er, at 44 spiller nemmere – du kan ramme et set og være tryg ved at spille for hele stacken. Med QJ kan du ramme top par og havne i svære spots postflop.

Dit spil bør ikke kun tilpasses efter ren ICM, men også efter hvordan dine modstandere tilpasser sig ICM. Her oplever jeg, at der ikke er så tydelige tendenser i playerpoolen som i andre situationer.

Du vil se både:

• Spillere der ikke forstår ICM, eller som ignorerer det og bare vil vinde trofæet.
• Spillere der er ekstremt forsigtige og bare gerne vil i pengene.

Derfor er det vigtigt at holde øje med showdowns og hvad folk siger ved bordet – det kan give dig indsigt i deres tilgang.

Et eksempel:
Hvis jeg er shortstack på boblen i en stor turnering, så spiller jeg endnu tightere end ICM ville anbefale. Det skyldes, at mange i playerpoolen begår store ICM-fejl og smider deres stack unødvendigt væk. Ved at være passiv kan jeg overrealisere min chance for at komme i pengene.

Omvendt – hvis jeg er bigstack – justerer jeg mit spil afhængigt af, hvordan andre har tilpasset sig. Har jeg spillere bag mig, der overjusterer som shortstacks og bare vil i pengene, kan jeg være overaggressiv – raise næsten 100% af hænderne eller lave store open-jams. Hvis spillerne ikke tilpasser sig ICM, så spiller jeg mere normalt mod dem.

Nogle gange som bigstack kan det føles uretfærdigt:

“Kæft, jeg har haft det hårdt så mange gange som shortstack på boblen, og nu er jeg endelig bigstack og burde kunne køre over dem. Men de er dumme og lader mig ikke gøre det!”

Bare rolig. Hvis nogen spiller suboptimalt, opstår der EV (forventet værdi) et andet sted. I det her tilfælde lander den hos shortstacks, der overrealiserer deres chance for at nå pengene. Så når du er shortstack mod sådanne spillere, så er det dig, der får den ekstra EV.

Finalebords-scenarie og beregning

Forestil dig følgende finalebord med ni spillere tilbage. Præmieudbetalingerne er taget fra sidste års DM, og stackstørrelserne er hypotetiske. Hvis vi siger at BB = 100.000, har vi følgende stacks i BB:
100, 45, 30, 25, 17, 12, 10, 8 og 5 – en ganske normal finalebordsfordeling.

Til højre ses ICM-værdien af hver stack.

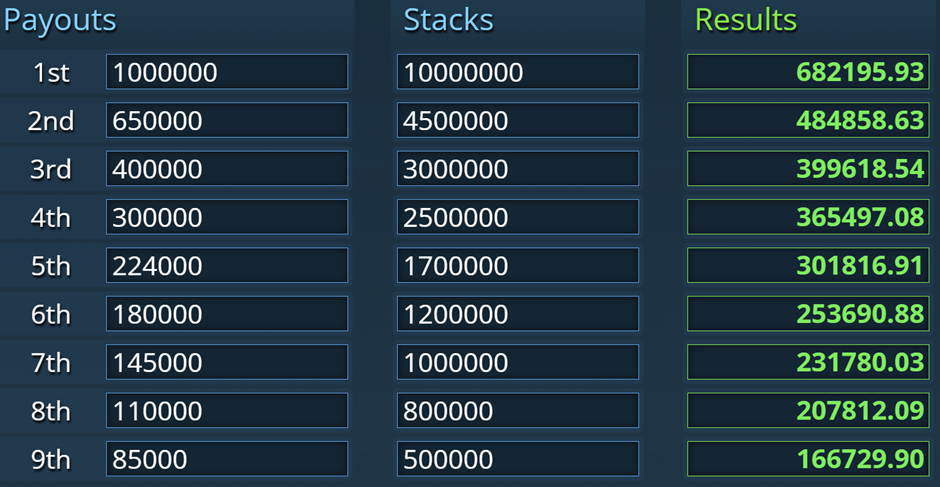
SB vs BB-scenarie

Lad os nu se på en hånd mellem chipleaderen og spilleren der på dette tidspunkt ligger på 5. pladsen (som vi kalder Hero) med 17 BB.

Hero sidder i BB og har allerede postet ante og big blind. Villain (chipleaderen) sidder i SB. Alle andre har foldet. Vi antager, at Villain går all-in med 100% af sin range. Spørgsmålet bliver:

Hvad kan Hero kalde med?

---

Som en lille træning for sig selv, vil jeg anbefale læseren at selv tænke over, hvilken range af hænder, man havde kaldt med i dette spot, før vi går videre og beregner os frem til svaret.

---

ICM-værdi ved fold bliver bare Heros ICM-værdi efter at have tabt 2 BB til Ante og BB. Denne kan vi se her:

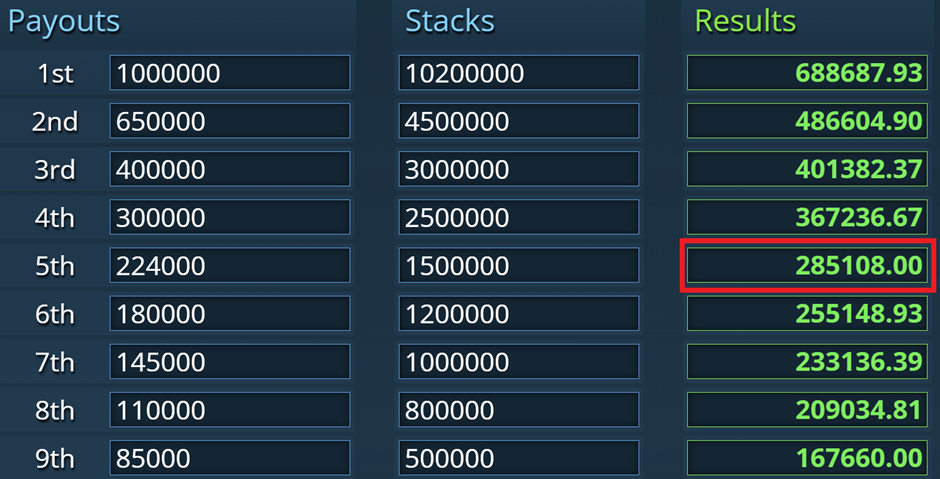
Så 285.108 DKK

Lad os se hvad ICM-værdien er hvis Hero kalder og vinder:

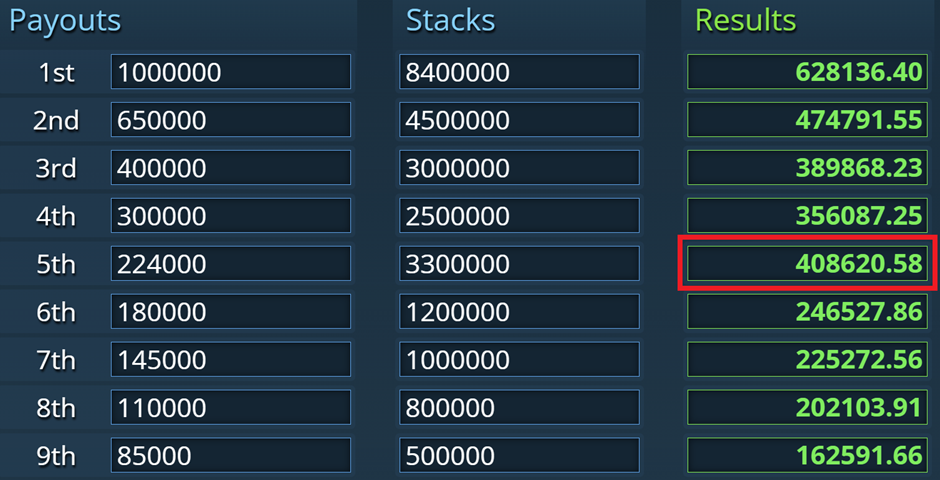
Så 408.620,58 DKK

ICM-værdien hvis Hero kalder og taber er selvfølgeligt 85.000 DKK siden Hero røger ud af turneringen 9. plads.

Lad os sige at P er sandsynligheden at Hero vinder hånden i det tilfælde Hero har kaldt.

EV ved kald bliver så: P*(ICM-værdi ved gevinst) + (1-P) 85.000.

Hvis vi skal finde et equilibrium hvor Hero er ligegyldig mellem at folde og kalde så skal vi løse følgende ligning:

P*408.620,58 + (1-P) 85.000 = 285.108

->   P (408.620,58 – 85.000) = 200.108

->   P = 200.108 / 323.620,58

->   P = 0,6183 = 61,83%

Det betyder altså at hvis Hero skal lave et +PengeEV kald, så skal Hero have mere end 61,83% chance at vinde hånden. Lad os kigge på, hvad for range man skal have for at have > 61,83% equity mod en 100% range.

Hvilke hænder kan vi kalde med og hvilke skal vi folde?

Hvis vi starter med at kigge på pocket pairs, så er 66 det lavest par som har equity over vores threshold for at kalde

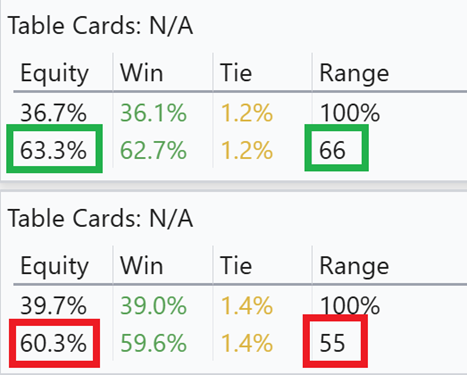
Hvis vi kigger på unpaired hands så har vi følgende threasholds

Suited esser

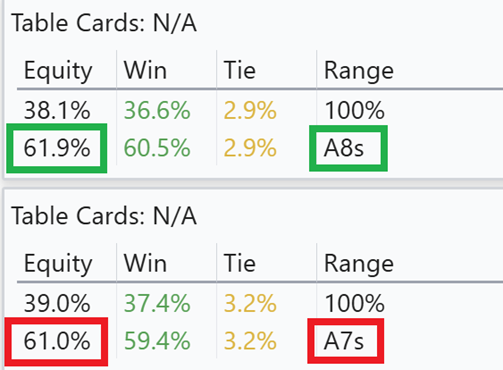
Offsuit esser

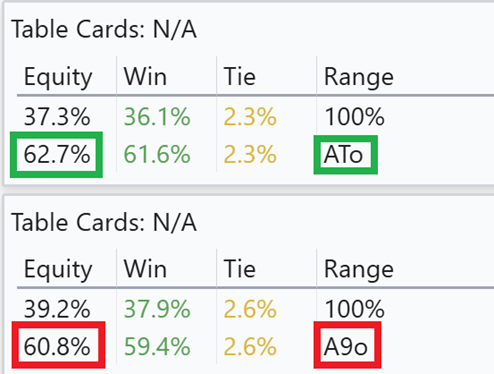
Suited konger

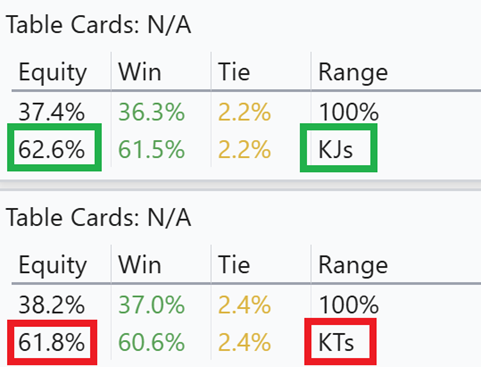
Og under kan vi se at det ikke findes offsuited konger eller suited damer som vi kan kalde profitabelt

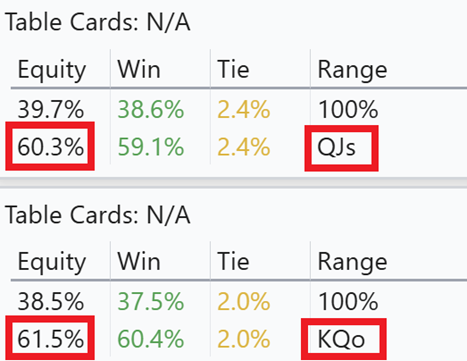
Den range hero kan kalde med for +PengeEV er så følgende range:

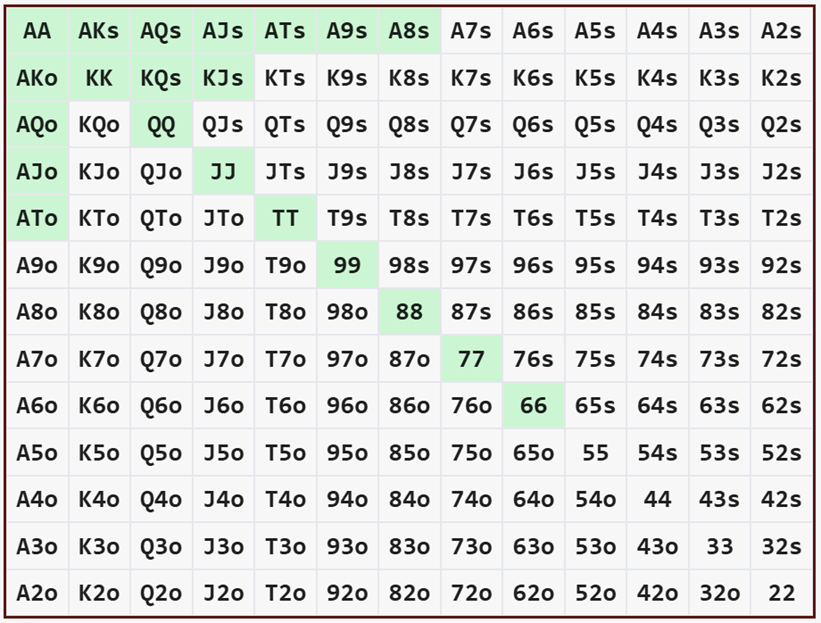
Dette svarer til 134 kombinationer ud af i alt 1.326 mulige kombinationer. Det vil sige 10,11% af Heros hænder. Så selvom Hero ved, at Villain går all-in med 100% af sine hænder, kan Hero – på grund af ICM – kun kalde med 10,11% af sine hænder.

Næste spørgsmål i analysen:

Kan Villain profitabelt gå all-in med 100% af sin range?

For at finde ud af det, skal vi beregne følgende udtryk, omsat til ord:

(Sandsynligheden for at Hero folder * Villains ICM-værdi i det udfald) +
(Sandsynligheden for at Hero kalder og vinder hånden * Villains ICM-værdi i det udfald) +
(Sandsynligheden for at Hero kalder og taber hånden * Villains ICM-værdi i det udfald)

…og derefter sammenligne det med Villains ICM-værdi hvis han folder.

Vi definerer følgende variabler:

• F = Sandsynligheden for at Hero folder mod Villains all-in
• P = Sandsynligheden for at Hero vinder hånden, hvis han kalder
• ICM_V_F = Villains ICM-værdi, hvis han folder
• ICM_H_F = Villains ICM-værdi, hvis Hero folder mod all-in
• ICM_K_T = Villains ICM-værdi, hvis Hero kalder og Villain taber hånden
• ICM_K_G = Villains ICM-værdi, hvis Hero kalder og Villain vinder hånden

Vi ønsker at finde ud af, hvilken værdi P skal have, for at følgende ulighed er sand:

F × ICM_H_F + (1-F) × P × ICM_K_T + (1-F) × (1-P) × ICM_K_G > ICM_V_F

Ud fra tidligere ICM-beregninger har vi:

• ICM_V_F = 680.564,65 DKK
• ICM_H_F = 688.687,93 DKK
• ICM_K_T = 628.136,40 DKK
• ICM_K_G = 735.862,46 DKK

Vi sætter ind de tal vi kender i vores formel

0,8989 * 688.687,93 + (1-0,8989) * P * 628.136,40 + (1-0,8989) * (1-P) * 735.862.46 > 680.564,65

->   619.421,37 + 63.478,01 * P + 74.381,59 – 74.381,59 * P > 680.564,65

->  10.903,58 * P < 13.238,31

Resultat

Her kan vi så se, at selv hvis vi sætter P = 1, det vil sige, at Hero vinder hånden 100 % af gangene, når det bliver showdown, så er det stadig 2.334,73 DKK mere profitabelt for Villain at gå all-in. At Villain selvfølgelig altid har noget equity ved et kald, er blot noget, der lægges oveni beregningen, hvilket gør et shove endnu mere profitabelt for Villain.

Så svaret er: Ja, Villain kan profitabelt gå all-in med 100 % af sin range.

Det er faktisk sådan, at den rene fold equity er nok til at kunne gå all-in profitabelt.

En sidenote til dette er, at Villain sandsynligvis kan skabe endnu mere profitable strategier ved også at inkludere non-all-in raises og limps. Dette må være en debat til en anden artikel. Men i denne artikel har vi kunnet matematisk bevise, at det er profitabelt for Villain at gå all-in med alle sine hænder – med den antagelse, at Hero forventer, at Villain gør netop dette, og derefter tilpasser sin calling-range til ICM.

Det er generelt ekstremt svært at finde ud af, hvordan et særligt spil påvirker din forventede penge-værdi, når ICM er involveret. Til forskel fra cashgames, hvor du kan nøjes med at regne på potodds og kombinationer. Med ICM kan et spil, som er +ChipEV, stadig være meget -PengeEV.

Det er tæt på umuligt at sidde ved bordet og forsøge at beregne sin ICM-værdi på et spil, og det er ikke noget, jeg anbefaler, man prøver at gøre. Det handler mere om at have kigget på mange forskellige scenarier som ovenstående og opbygget en erfaring og et instinkt for, hvordan man skal tilpasse sine ranges i forskellige scenarier – og så stole på det instinkt ved bordet.

Held og lykke på dit næste finalebord eller boblespil!

Marcus Wuttke

Marcus Wuttke til MPT Main Event 2025 dag 2

---

Denne artikel på Dansk Poker er sponsoreret af Pladebixen.dk